5.4 欧拉方程；正则奇点

在本节中，我们将开始考虑如何求解以下形式的方程：

P(x)y′′+Q(x)y′+R(x)y=0\begin{equation*} P(x) y^{\prime \prime}+Q(x) y^{\prime}+R(x) y=0 \tag{1} \end{equation*}

在奇点 x0x_{0} 附近。 回忆一下，如果函数 P,QP, Q 和 RR 是多项式，并且它们没有共同的因子，那么方程 (1) 的奇点就是使 P(x)=0P(x)=0 的点。

欧拉方程。 具有奇点的相对简单的微分方程是欧拉方程 10{ }^{10}

L[y]=x2y′′+αxy′+βy=0\begin{equation*} L[y]=x^{2} y^{\prime \prime}+\alpha x y^{\prime}+\beta y=0 \tag{2} \end{equation*}

其中 α\alpha 和 β\beta 是实常数。 那么 P(x)=x2,Q(x)=αxP(x)=x^{2}, Q(x)=\alpha x, 和 R(x)=βR(x)=\beta。 如果 β≠0\beta \neq 0，那么 P(x),Q(x)P(x), Q(x) 和 R(x)R(x) 没有公因子，因此方程 (2) 的唯一奇点是 x=0x=0；所有其他点都是常点。 为了方便起见，我们首先考虑区间 x>0x>0；稍后我们将结果扩展到区间 x<0x<0。

观察到 (xr)′=rxr−1\left(x^{r}\right)^{\prime}=r x^{r-1} 且 (xr)′′=r(r−1)xr−2\left(x^{r}\right)^{\prime \prime}=r(r-1) x^{r-2}。 因此，如果我们假设方程 (2) 具有以下形式的解

y=xr\begin{equation*} y=x^{r} \tag{3} \end{equation*}

那么我们得到

L[xr]=x2(xr)′′+αx(xr)′+βxr=x2r(r−1)xr−2+αx(rxr−1)+βxr=xr(r(r−1)+αr+β).\begin{align*} L\left[x^{r}\right] & =x^{2}\left(x^{r}\right)^{\prime \prime}+\alpha x\left(x^{r}\right)^{\prime}+\beta x^{r} \\ & =x^{2} r(r-1) x^{r-2}+\alpha x\left(r x^{r-1}\right)+\beta x^{r} \\ & =x^{r}(r(r-1)+\alpha r+\beta) . \tag{4} \end{align*}

如果 rr 是二次方程的根

F(r)=r(r−1)+αr+β=0\begin{equation*} F(r)=r(r-1)+\alpha r+\beta=0 \tag{5} \end{equation*}

那么 L[xr]L\left[x^{r}\right] 为零，并且 y=xry=x^{r} 是方程 (2) 的解。 方程 (5) 的根为

r1,r2=−(α−1)±(α−1)2−4β2\begin{equation*} r_{1}, r_{2}=\frac{-(\alpha-1) \pm \sqrt{(\alpha-1)^{2}-4 \beta}}{2} \tag{6} \end{equation*}

并且方程（5）中定义的二次多项式 F(r)F(r) 也可以写成 F(r)=F(r)= (r−r1)(r−r2)\left(r-r_{1}\right)\left(r-r_{2}\right)。 模仿常系数二阶线性微分方程的处理方式，我们分别考虑根是实数且不同、实数但相等以及复共轭的情况。 实际上，欧拉方程的整个讨论与第 3 章中常系数二阶线性方程的处理方式相似，只是将 erxe^{r x} 替换为 xrx^{r}。

实数，不同的根。 如果 F(r)=0F(r)=0 具有实根 r1r_{1} 和 r2r_{2}，其中 r1≠r2r_{1} \neq r_{2}，那么 y1(x)=xr1y_{1}(x)=x^{r_{1}} 和 y2(x)=xr2y_{2}(x)=x^{r_{2}} 是方程 (2) 的解。 因为

W[xr1,xr2]=(r2−r1)xr1+r2−1W\left[x^{r_{1}}, x^{r_{2}}\right]=\left(r_{2}-r_{1}\right) x^{r_{1}+r_{2}-1}

对于 r1≠r2r_{1} \neq r_{2} 和 x>0x>0 非零，因此方程 (2) 的通解是

y=c1xr1+c2xr2,x>0.\begin{equation*} y=c_{1} x^{r_{1}}+c_{2} x^{r_{2}}, \quad x>0 . \tag{7} \end{equation*}

注意，如果 rr 不是有理数，那么 xrx^{r} 由 xr=erln⁡xx^{r}=e^{r \ln x} 定义。

示例 1

求解

2x2y′′+3xy′−y=0,x>0\begin{equation*} 2 x^{2} y^{\prime \prime}+3 x y^{\prime}-y=0, \quad x>0 \tag{8} \end{equation*}

[^7]

解：

将 y=xry=x^{r} 代入方程 (8) 得到

xr(2r(r−1)+3r−1)=xr(2r2+r−1)=xr(2r−1)(r+1)=0.x^{r}(2 r(r-1)+3 r-1)=x^{r}\left(2 r^{2}+r-1\right)=x^{r}(2 r-1)(r+1)=0 .

因此 r1=12r_{1}=\frac{1}{2} 和 r2=−1r_{2}=-1，所以方程 (8) 的通解是

y=c1x1/2+c2x−1,x>0.\begin{equation*} y=c_{1} x^{1 / 2}+c_{2} x^{-1}, \quad x>0 . \tag{9} \end{equation*}

相等根。 如果根 r1r_{1} 和 r2r_{2} 相等，那么我们只能得到一个形式为 y1(x)=xr1y_{1}(x)=x^{r_{1}} 的解。 第二个解可以通过降阶法获得，但是为了我们以后的讨论，我们考虑一种替代方法。 因为 r1=r2r_{1}=r_{2}，所以 F(r)=(r−r1)2F(r)=\left(r-r_{1}\right)^{2}。 因此，在这种情况下，不仅 F(r1)=0F\left(r_{1}\right)=0 而且 F′(r1)=0F^{\prime}\left(r_{1}\right)=0。 这建议对方程 (4) 关于 rr 求导，然后将 rr 设置为 r1r_{1}。 通过对方程 (4) 关于 rr 求导，我们得到

∂∂rL[xr]=∂∂r[xrF(r)]=∂∂r[xr(r−r1)2]=(r−r1)2xrln⁡x+2(r−r1)xr\begin{align*} \frac{\partial}{\partial r} L\left[x^{r}\right] & =\frac{\partial}{\partial r}\left[x^{r} F(r)\right]=\frac{\partial}{\partial r}\left[x^{r}\left(r-r_{1}\right)^{2}\right] \\ & =\left(r-r_{1}\right)^{2} x^{r} \ln x+2\left(r-r_{1}\right) x^{r} \tag{10} \end{align*}

然而，通过交换对 xx 的微分和对 rr 的微分，我们也可以得到

∂∂rL[xr]=L[∂∂rxr]=L[xrln⁡x]\frac{\partial}{\partial r} L\left[x^{r}\right]=L\left[\frac{\partial}{\partial r} x^{r}\right]=L\left[x^{r} \ln x\right]

方程 (10) 的右侧对于 r=r1r=r_{1} 为零； 因此，L[xr1ln⁡x]=0L\left[x^{r_{1}} \ln x\right]=0 也成立。 因此，方程 (2) 的第二个解是

y2(x)=xr1ln⁡x,x>0\begin{equation*} y_{2}(x)=x^{r_{1}} \ln x, \quad x>0 \tag{11} \end{equation*}

通过计算 y1y_{1} 和 y2y_{2} 的 Wronskian 行列式，我们发现

W[xr1,xr1ln⁡x]=x2r1−1.W\left[x^{r_{1}}, x^{r_{1}} \ln x\right]=x^{2 r_{1}-1} .

因此，xr1x^{r_{1}} 和 xr1ln⁡xx^{r_{1}} \ln x 是 x>0x>0 时方程 (2) 的一个基本解集，方程 (2) 的通解为

y=(c1+c2ln⁡x)xr1,x>0\begin{equation*} y=\left(c_{1}+c_{2} \ln x\right) x^{r_{1}}, \quad x>0 \tag{12} \end{equation*}

示例 2

解

x2y′′+5xy′+4y=0,x>0\begin{equation*} x^{2} y^{\prime \prime}+5 x y^{\prime}+4 y=0, \quad x>0 \tag{13} \end{equation*}

解：

将 y=xry=x^{r} 代入方程 (13) 得到

xr(r(r−1)+5r+4)=xr(r2+4r+4)=0.x^{r}(r(r-1)+5 r+4)=x^{r}\left(r^{2}+4 r+4\right)=0 .

因此 r1=r2=−2r_{1}=r_{2}=-2，并且

y=x−2(c1+c2ln⁡x),x>0\begin{equation*} y=x^{-2}\left(c_{1}+c_{2} \ln x\right), \quad x>0 \tag{14} \end{equation*}

是方程 (13) 的通解。

复数根。最后，假设方程 (5) 的根 r1r_{1} 和 r2r_{2} 是复共轭，比如，r1=λ+iμr_{1}=\lambda+i \mu 和 r2=λ−iμr_{2}=\lambda-i \mu，其中 μ≠0\mu \neq 0。我们现在必须解释当 rr 是复数时，xrx^{r} 是什么意思。记住

xr=erln⁡x\begin{equation*} x^{r}=e^{r \ln x} \tag{15} \end{equation*}

当 x>0x>0 且 rr 是实数时，我们可以使用这个方程来定义当 rr 是复数时 xrx^{r}。然后，使用欧拉公式 eiμln⁡xe^{i \mu \ln x}，我们得到

xλ+iμ=e(λ+iμ)ln⁡x=eλln⁡xeiμln⁡x=xλeiμln⁡x=xλ(cos⁡(μln⁡x)+isin⁡(μln⁡x)),x>0.\begin{align*} x^{\lambda+i \mu}=e^{(\lambda+i \mu) \ln x} & =e^{\lambda \ln x} e^{i \mu \ln x}=x^{\lambda} e^{i \mu \ln x} \\ & =x^{\lambda}(\cos (\mu \ln x)+i \sin (\mu \ln x)), \quad x>0 . \tag{16} \end{align*}

对于复数 rr 值的 xrx^{r} 的这种定义，可以验证代数和微分的常用法则都成立，因此 xr1x^{r_{1}} 和 xr2x^{r_{2}} 确实是方程 (2) 的解。方程 (2) 的通解是

y=c1xλ+iμ+c2xλ−iμ\begin{equation*} y=c_{1} x^{\lambda+i \mu}+c_{2} x^{\lambda-i \mu} \tag{17} \end{equation*}

这种表达的缺点是函数 xλ+iμx^{\lambda+i \mu} 和 xλ−iμx^{\lambda-i \mu} 是复数值的。回想一下，当特征方程的根是复数时，对于具有常系数的二阶微分方程，我们遇到了类似的情况。正如我们当时所做的那样，我们可以使用定理 3.2.6 通过取 xλ+iμx^{\lambda+i \mu} 的实部和虚部，即，来获得方程 (2) 的实值解

xλcos⁡(μln⁡x) 和 xλsin⁡(μln⁡x)\begin{equation*} x^{\lambda} \cos (\mu \ln x) \text { 和 } x^{\lambda} \sin (\mu \ln x) \tag{18} \end{equation*}

一个简单的计算表明（见问题 29）

W[xλcos⁡(μln⁡x),xλsin⁡(μln⁡x)]=μx2λ−1.W\left[x^{\lambda} \cos (\mu \ln x), x^{\lambda} \sin (\mu \ln x)\right]=\mu x^{2 \lambda-1} .

因此，这些解构成了 x>0x>0 的一个基本解集，欧拉方程 (2) 的通解为

y=c1xλcos⁡(μln⁡x)+c2xλsin⁡(μln⁡x),x>0\begin{equation*} y=c_{1} x^{\lambda} \cos (\mu \ln x)+c_{2} x^{\lambda} \sin (\mu \ln x), \quad x>0 \tag{19} \end{equation*}

示例 3

解

x2y′′+xy′+y=0.\begin{equation*} x^{2} y^{\prime \prime}+x y^{\prime}+y=0 . \tag{20} \end{equation*}

解：

将 y=xry=x^{r} 代入方程 (20) 得到

x^{r}(r(r-1)+r+1)=x^{r}\left(r^{2}+1\right)=0 .

因此 $r= \pm i$，**通解**为

\begin{equation*} y=c_{1} \cos (\ln x)+c_{2} \sin (\ln x), \quad x>0 . \tag{21} \end{equation*}

**因子** $x^{\lambda}$ 没有在**方程** (21) 中显式出现，因为在这个**例子**中 $\lambda=0$ 且 $x^{\lambda}=1$。 现在让我们考虑**方程** (2) 的**解**在**奇点** $x=0$ 附近的**定性行为**。这完全取决于**指数** $r_{1}$ 和 $r_{2}$ 的**值**。首先，如果 $r$ 是**实数**且为正，那么当 $x$ 通过正**值**趋于**零**时，$x^{r} \rightarrow 0$。另一方面，如果 $r$ 是**实数**且为**负数**，那么 $x^{r}$ 变得无界。最后，如果 $r=0$，那么 $x^{r}=1$。**图** 5.4.1 显示了 $r$ 的各种**值**的这些**可能性**。如果 $r$ 是**复数**，那么一个典型的**解**是 $x^{\lambda} \cos (\mu \ln x)$。如果 $\lambda$ 是**负数**或正数，则该**函数**会变得无界或接近于**零**，并且当 $x \rightarrow 0$ 时，**振荡**也会越来越快。**图** 5.4.2 和 5.4.3 显示了 $\lambda$ 和 $\mu$ 的选定**值**的这种**行为**。如果 $\lambda=0$，则**振荡幅度**恒定。最后，如果存在**重复根**，那么一个**解**的**形式**为 $x^{r} \ln x$，如果 $r>0$，则趋于**零**，如果 $r \leq 0$，则变得无界。**图** 5.4.4 显示了每种**情况**的一个**例子**。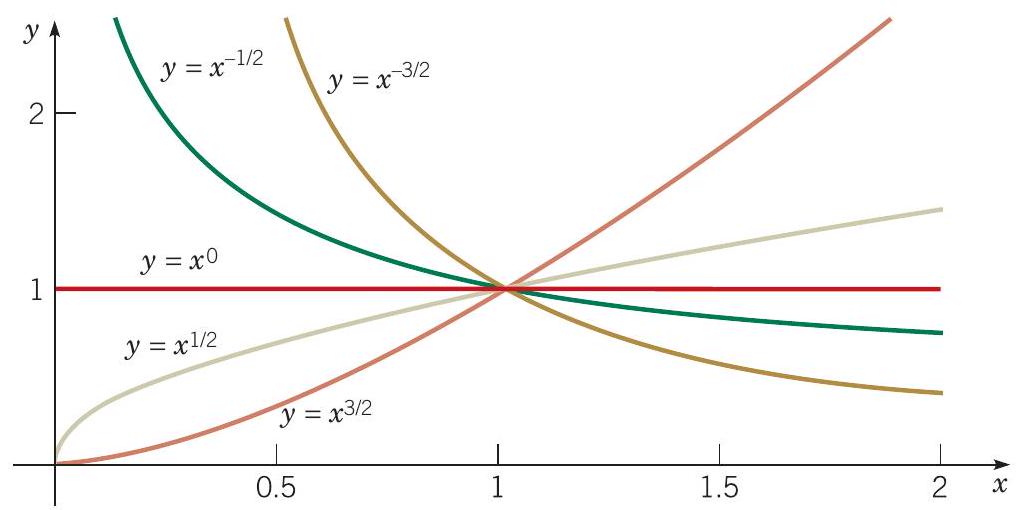 ![](https://cdn.mathpix.com/cropped/2025_02_01_44b8118dd7565fd86bfdg-26.jpg?height=510&width=1021&top_left_y=130&top_left_x=761) **图** 5.4.1 **欧拉方程**的**解**；**实根** $(\mu=0)$。 ![](https://cdn.mathpix.com/cropped/2025_02_01_44b8118dd7565fd86bfdg-26.jpg?height=397&width=636&top_left_y=821&top_left_x=517) **图** 5.4.2 **欧拉方程**的**解**；具有**负实部**的**复数根**。 ![](https://cdn.mathpix.com/cropped/2025_02_01_44b8118dd7565fd86bfdg-26.jpg?height=397&width=590&top_left_y=821&top_left_x=1278) **图** 5.4.3 **欧拉方程**的**解**；具有**正实部**的**复数根**。 ![](https://cdn.mathpix.com/cropped/2025_02_01_44b8118dd7565fd86bfdg-26.jpg?height=408&width=609&top_left_y=1404&top_left_x=970) **图** 5.4.4 具有**等根**的**欧拉方程**的两个典型**第二解**：$r>0$（**红色**），$r<0$（**蓝色**）。 **方程** (2) 的**解**扩展到**区间** $x<0$ 可以以相对直接的**方式**进行。**困难**在于理解当 $x$ 为**负**且 $r$ 不是**整数**时，$x^{r}$ 的**含义**；类似地，$\ln x$ 尚未为 $x<0$ 定义。我们给出的 $x>0$ 时**欧拉方程**的**解**可以证明对于 $x<0$ 也是有效的，但一般来说，它们是**复数值**的。因此，在**例** 1 中，**解** $x^{1 / 2}$ 对于 $x<0$ 是虚数的。 总是可以通过进行以下**变量替换**来获得**区间** $x<0$ 中**欧拉方程** (2) 的**实数值解**。令 $x=-\xi$，其中 $\xi>0$，并令 $y=u(\xi)$。那么我们有

\begin{equation*} \frac{d y}{d x}=\frac{d u}{d \xi} \frac{d \xi}{d x}=-\frac{d u}{d \xi}, \quad \frac{d^{2} y}{d x^{2}}=\frac{d}{d \xi}\left(-\frac{d u}{d \xi}\right) \frac{d \xi}{d x}=\frac{d^{2} u}{d \xi^{2}} \tag{22} \end{equation*}

因此，对于 $x<0$，**方程** (2) 变为

\begin{equation*} \xi^{2} \frac{d^{2} u}{d \xi^{2}}+\alpha \xi \frac{d u}{d \xi}+\beta u=0, \quad \xi>0 \tag{23} \end{equation*}

但除了∗∗变量∗∗的∗∗名称∗∗之外，这与∗∗方程∗∗(2)完全相同；从∗∗方程∗∗(7)、(12)和(19)中，我们有 但除了**变量**的**名称**之外，这与**方程** (2) 完全相同；从**方程** (7)、(12) 和 (19) 中，我们有

u(\xi)= \begin{cases}c_{1} \xi^{r_{1}}+c_{2} \xi^{r_{2}} & \text { 如果 } r_{1} \text { 和 } r_{2} \text { 是实数值且不同的 } \tag{24}\ \left(c_{1}+c_{2} \ln \xi\right) \xi^{r_{1}} & \text { 如果 } r_{1} \text { 和 } r_{2} \text { 是实数值且 } r_{1}=r_{2} \ c_{1} \xi^{\lambda} \cos (\mu \ln \xi)+c_{2} \xi^{\lambda} \sin (\mu \ln \xi) & \text { 如果 } r_{1,2}=\lambda \pm i \mu \text { 是复数值的 } \ & (\mu \neq 0)\end{cases}

取决于 $F(r)=r(r-1)+\alpha r+\beta=0$ 的**零点**的**性质**。要用 $x$ 表示 $u$，我们在**方程** (24) 中用 $-x$ 替换 $\xi$。 我们可以通过回忆 $|x|=x$ 当 $x>0$ 且 $|x|=-x$ 当 $x<0$ 来组合 $x>0$ 和 $x<0$ 的**结果**。因此，我们只需要在**方程** (7)、(12) 和 (19) 中用 $|x|$ 替换 $x$，即可获得在任何不包含**原点**的**区间**内都有效的**实数值解**。 因此，**欧拉方程** (2)

x^{2} y^{\prime \prime}+\alpha x y^{\prime}+\beta y=0

在任何不包含∗∗原点∗∗的∗∗区间∗∗内的∗∗通解∗∗由∗∗方程∗∗ 在任何不包含**原点**的**区间**内的**通解**由**方程**

F(r)=r(r-1)+\alpha r+\beta=0

的**根** $r_{1}$ 和 $r_{2}$ 确定如下。如果**根** $r_{1}$ 和 $r_{2}$ 是**实数**且不同的，$r_{1,2}=\lambda \pm i \mu$，则

\begin{equation*} y=c_{1}|x|^{r_{1}}+c_{2}|x|^{r_{2}} . \tag{25} \end{equation*}

如果∗∗根∗∗是∗∗实数∗∗且相等的，则 如果**根**是**实数**且相等的，则

\begin{equation*} y=\left(c_{1}+c_{2} \ln |x|\right)|x|^{r_{1}} . \tag{26} \end{equation*}

如果**根**是**复共轭**，$r_{1,2}=\lambda \pm i \mu$，则

\begin{equation*} y=|x|^{\lambda}\left(c_{1} \cos (\mu \ln |x|)+c_{2} \sin (\mu \ln |x|)\right) . \tag{27} \end{equation*}

∗∗形式∗∗为 **形式**为

\begin{equation*} \left(x-x_{0}\right)^{2} y^{\prime \prime}+\alpha\left(x-x_{0}\right) y^{\prime}+\beta y=0 \tag{28} \end{equation*}

的**欧拉方程**的**解**是相似的。如果我们寻找 $y=\left(x-x_{0}\right)^{r}$ **形式**的**解**，那么**通解**由**方程** (25)、**方程** (26) 或**方程** (27) 给出，其中 $x$ 被 $x-x_{0}$ 替换。或者，我们可以通过改变**自变量** $t=x-x_{0}$ 将**方程** (28) 简化为**方程** (2) 的**形式**。 **正则奇点**。现在我们回到对一般**方程** (1) 的考虑

P(x) y^{\prime \prime}+Q(x) y^{\prime}+R(x) y=0

其中 $x_{0}$ 是一个**奇点**。这意味着 $P\left(x_{0}\right)=0$ 并且 $Q$ 和 $R$ 中至少有一个在 $x_{0}$ 处不为**零**。 不幸的是，如果我们尝试使用前两节的**方法**来求解**奇点** $x_{0}$ 附近的**方程** (1)，我们会发现这些**方法**失败了。这是因为**方程** (1) 的**解**通常在 $x_{0}$ 处不是解析的，因此不能用 $x-x_{0}$ 的**幂**的**泰勒级数**表示。**例** 1、2 和 3 说明了这一**事实**；在这些**例子**中，**解**都无法在**奇点** $x=0$ 附近进行**幂级数展开**。因此，为了有机会求解**奇点**附近的**方程** (1)，我们必须使用更一般的**级数展开式**。 由于**微分方程**的**奇点**通常**数量**较少，我们可能会问是否可以简单地忽略它们，特别是因为我们已经知道如何构造关于**常点**的**解**。然而，这是不可行的。**奇点**在很大程度上决定了**解**的**主要特征**，其**程度**远超你最初的设想。在**奇点**附近，**解**的**幅度**通常会变得很大，或者**幅度**发生快速变化。例如，**例** 1、2 和 3 中找到的**解**就是对这一**事实**的**例证**。因此，由**微分方程**建模的**物理系统**的**行为**通常在**奇点**附近最有趣。通常，**物理问题**中的**几何奇点**（例如**角**或**锐边**）会导致相应**微分方程**中的**奇点**。因此，尽管起初我们可能想避免**微分方程**的少数几个**奇点**，但恰恰是在这些**点**上，我们最有必要仔细研究**解**。 作为**解析方法**的**替代方案**，我们可以考虑使用**数值方法**，这将在第 8 **章**中讨论。然而，这些**方法**不太适合研究**奇点**附近的**解**。因此，即使我们采用**数值方法**，为了检查**奇点**附近**解**的**行为**，最好将其与本**章**的**分析方法**结合使用。 如果没有关于 $Q / P$ 和 $R / P$ 在**奇点**附近的任何额外**信息**，就不可能描述**方程** (1) 的**解**在 $x=x_{0}$ 附近的**行为**。可能是**方程** (1) 有两个不同的**解**在 $x \rightarrow x_{0}$ 时保持有界（如**例** 3 所示）；也可能只有一个，而另一个在 $x \rightarrow x_{0}$ 时变得无界（如**例** 1 所示）；或者它们可能都在 $x \rightarrow x_{0}$ 时变得无界（如**例** 2 所示）。如果**方程** (1) 有在 $x \rightarrow x_{0}$ 时变得无界的**解**，那么确定这些**解**在 $x \rightarrow x_{0}$ 时如何变化通常很重要。例如，$y \rightarrow \infty$ 的**方式**是否与 $\left(x-x_{0}\right)^{-1}$ 或 $\left|x-x_{0}\right|^{-1 / 2}$ 相同，或者以其他**方式**？ 我们的**目标**是扩展已经开发的用于求解**常点**附近**方程** (1) 的**方法**，使其也适用于**奇点** $x_{0}$ 附近。为了以一种相对简单的**方式**做到这一点，有必要将自己限制在**函数** $Q / P$ 和 $R / P$ 在 $x=x_{0}$ 处的**奇点**不太严重的**情况**下——也就是说，限制在我们可能称之为“**弱奇点**”的**情况**下。在这个**阶段**，还不清楚什么是可接受的**奇点**。但是，随着我们开发求解**方法**，你将会看到区分“**弱奇点**”的适当**条件**（另见第 5.6 节，**问题** 16）是

\begin{equation*} \lim {x \rightarrow x{0}}\left(x-x_{0}\right) \frac{Q(x)}{P(x)} \text { 是有限的 } \tag{29} \end{equation*}

和 和

\begin{equation*} \lim {x \rightarrow x{0}}\left(x-x_{0}\right)^{2} \frac{R(x)}{P(x)} \text { 是有限的. } \tag{30} \end{equation*}

这意味着 $Q / P$ 中的**奇点**不能比 $\left(x-x_{0}\right)^{-1}$ 更糟，并且 $R / P$ 中的**奇点**不能比 $\left(x-x_{0}\right)^{-2}$ 更糟。这样的**点**称为**方程** (1) 的**正则奇点**。对于**系数**比**多项式**更一般的**方程**，$x_{0}$ 是**方程** (1) 的**正则奇点**，如果它是一个**奇点**并且如果 ${ }^{11}$ “ \left(x-x_{0}\right) \frac{Q(x)}{P(x)} \text { 和 }\left(x-x_{0}\right)^{2} \frac{R(x)}{P(x)} \tag{31} \end{equation*}

在 x0x_{0} 附近具有收敛的泰勒级数——也就是说，如果方程 (31) 中的函数在 x=x0x=x_{0} 处是解析的。当 P,QP, Q 和 RR 是多项式时，方程 (29) 和 (30) 意味着这种情况将会发生。方程 (1) 的任何不是正则奇点的奇点都称为方程 (1) 的非正则奇点。 [^8] 观察到 Euler 方程 (28) 满足方程 (29) 和 (30) 中的条件。因此，Euler 方程中的奇点是一个正则奇点。事实上，我们将看到所有形式为 (1) 的方程在正则奇点附近的行为非常类似于 Euler 方程。也就是说，正则奇点附近的解可能包括具有负或非整数指数的 xx 的幂、对数或对数自变量的正弦或余弦。 在接下来的章节中，我们将讨论如何在正则奇点附近求解方程 (1)。关于非正则奇点附近的微分方程的解的讨论更为复杂，可以在更高级的书中找到。

例 4

确定勒让德方程的奇点

(1−x2)y′′−2xy′+α(α+1)y=0\begin{equation*} \left(1-x^{2}\right) y^{\prime \prime}-2 x y^{\prime}+\alpha(\alpha+1) y=0 \tag{32} \end{equation*}

并确定它们是正则的还是非正则的。

解：

在这种情况下，P(x)=1−x2P(x)=1-x^{2}，所以奇点是 x=1x=1 和 x=−1x=-1。观察到当我们用 1−x21-x^{2} 除方程 (32) 时，y′y^{\prime} 和 yy 的系数分别是 −2x/(1−x2)-2 x /\left(1-x^{2}\right) 和 α(α+1)/(1−x2)\alpha(\alpha+1) /\left(1-x^{2}\right)。我们首先考虑点 x=1x=1。因此，从方程 (29) 和 (30)，我们计算

lim⁡x→1(x−1)−2x1−x2=lim⁡x→1(x−1)(−2x)(1−x)(1+x)=lim⁡x→12x1+x=1\lim _{x \rightarrow 1}(x-1) \frac{-2 x}{1-x^{2}}=\lim _{x \rightarrow 1} \frac{(x-1)(-2 x)}{(1-x)(1+x)}=\lim _{x \rightarrow 1} \frac{2 x}{1+x}=1

和

lim⁡x→1(x−1)2α(α+1)1−x2=lim⁡x→1(x−1)2α(α+1)(1−x)(1+x)=lim⁡x→1(x−1)(−α)(α+1)1+x=0.\begin{aligned} \lim _{x \rightarrow 1}(x-1)^{2} \frac{\alpha(\alpha+1)}{1-x^{2}} & =\lim _{x \rightarrow 1} \frac{(x-1)^{2} \alpha(\alpha+1)}{(1-x)(1+x)} \\ & =\lim _{x \rightarrow 1} \frac{(x-1)(-\alpha)(\alpha+1)}{1+x}=0 . \end{aligned}

由于这些极限是有限的，所以点 x=1x=1 是一个正则奇点。 可以用类似的方式证明 x=−1x=-1 也是一个正则奇点。

示例 5

确定微分方程

2x(x−2)2y′′+3xy′+(x−2)y=02 x(x-2)^{2} y^{\prime \prime}+3 x y^{\prime}+(x-2) y=0

的奇点，并将它们分类为正则的或非正则的。

解：

用 2x(x−2)22 x(x-2)^{2} 除微分方程，我们得到

y′′+32(x−2)2y′+12x(x−2)y=0,y^{\prime \prime}+\frac{3}{2(x-2)^{2}} y^{\prime}+\frac{1}{2 x(x-2)} y=0,

所以 p(x)=Q(x)P(x)=32(x−2)2p(x)=\frac{Q(x)}{P(x)}=\frac{3}{2(x-2)^{2}} 且 q(x)=R(x)P(x)=12x(x−2)q(x)=\frac{R(x)}{P(x)}=\frac{1}{2 x(x-2)}。奇点是 x=0x=0 和 x=2x=2。 考虑 x=0x=0。 我们有

lim⁡x→0xp(x)=lim⁡x→0x32(x−2)2=0,\lim _{x \rightarrow 0} x p(x)=\lim _{x \rightarrow 0} x \frac{3}{2(x-2)^{2}}=0,

和

lim⁡x→0x2q(x)=lim⁡x→0x212x(x−2)=0\lim _{x \rightarrow 0} x^{2} q(x)=\lim _{x \rightarrow 0} x^{2} \frac{1}{2 x(x-2)}=0

由于这些极限是有限的，所以 x=0x=0 是一个正则奇点。 对于 x=2x=2 我们有

lim⁡x→2(x−2)p(x)=lim⁡x→2(x−2)32(x−2)2=lim⁡x→232(x−2),\lim _{x \rightarrow 2}(x-2) p(x)=\lim _{x \rightarrow 2}(x-2) \frac{3}{2(x-2)^{2}}=\lim _{x \rightarrow 2} \frac{3}{2(x-2)},

所以极限不存在；因此 x=2x=2 是一个非正则奇点。

示例 6

确定

(x−π2)2y′′+(cos⁡x)y′+(sin⁡x)y=0\left(x-\frac{\pi}{2}\right)^{2} y^{\prime \prime}+(\cos x) y^{\prime}+(\sin x) y=0

的奇点，并将它们分类为正则的或非正则的。

解：

唯一的奇点是 x=π2x=\frac{\pi}{2}。为了研究它，我们考虑函数

(x−π2)p(x)=(x−π2)Q(x)P(x)=cos⁡xx−π/2\left(x-\frac{\pi}{2}\right) p(x)=\left(x-\frac{\pi}{2}\right) \frac{Q(x)}{P(x)}=\frac{\cos x}{x-\pi / 2}

和

(x−π2)2q(x)=(x−π2)2R(x)P(x)=sin⁡x\left(x-\frac{\pi}{2}\right)^{2} q(x)=\left(x-\frac{\pi}{2}\right)^{2} \frac{R(x)}{P(x)}=\sin x

从 cos⁡x\cos x 关于 x=π2x=\frac{\pi}{2} 的泰勒级数开始，我们发现

cos⁡xx−π/2=−1+(x−π/2)23!−(x−π/2)45!+⋯ ,\frac{\cos x}{x-\pi / 2}=-1+\frac{(x-\pi / 2)^{2}}{3!}-\frac{(x-\pi / 2)^{4}}{5!}+\cdots,

它对所有 xx 收敛。类似地，sin⁡x\sin x 在 x=π2x=\frac{\pi}{2} 处是解析的。因此，我们得出结论，π2\frac{\pi}{2} 是这个方程的正则奇点。

问题

在问题 1 到 8 中，确定给定微分方程的通解，该通解在不包含奇点的任何区间内有效。

  1. x2y′′+4xy′+2y=0x^{2} y^{\prime \prime}+4 x y^{\prime}+2 y=0
  2. (x+1)2y′′+3(x+1)y′+0.75y=0(x+1)^{2} y^{\prime \prime}+3(x+1) y^{\prime}+0.75 y=0
  3. x2y′′−3xy′+4y=0x^{2} y^{\prime \prime}-3 x y^{\prime}+4 y=0
  4. x2y′′−xy′+y=0x^{2} y^{\prime \prime}-x y^{\prime}+y=0
  5. x2y′′+6xy′−y=0x^{2} y^{\prime \prime}+6 x y^{\prime}-y=0
  6. 2x2y′′−4xy′+6y=02 x^{2} y^{\prime \prime}-4 x y^{\prime}+6 y=0
  7. x2y′′−5xy′+9y=0x^{2} y^{\prime \prime}-5 x y^{\prime}+9 y=0
  8. (x−2)2y′′+5(x−2)y′+8y=0(x-2)^{2} y^{\prime \prime}+5(x-2) y^{\prime}+8 y=0 在问题 9 到 11 中，找到给定初值问题的解。绘制解的图，并描述解如何随 x→0x \rightarrow 0 变化。 G 9. 2x2y′′+xy′−3y=0,y(1)=1,y′(1)=42 x^{2} y^{\prime \prime}+x y^{\prime}-3 y=0, \quad y(1)=1, \quad y^{\prime}(1)=4 G 10. 4x2y′′+8xy′+17y=0,y(1)=2,y′(1)=−34 x^{2} y^{\prime \prime}+8 x y^{\prime}+17 y=0, \quad y(1)=2, \quad y^{\prime}(1)=-3 (G) 11. x2y′′−3xy′+4y=0,y(−1)=2,y′(−1)=3x^{2} y^{\prime \prime}-3 x y^{\prime}+4 y=0, \quad y(-1)=2, \quad y^{\prime}(-1)=3 在问题 12 到 23 中，找到给定方程的所有奇点，并确定每个奇点是正则的还是非正则的。
  9. xy′′+(1−x)y′+xy=0x y^{\prime \prime}+(1-x) y^{\prime}+x y=0
  10. x2(1−x)2y′′+2xy′+4y=0x^{2}(1-x)^{2} y^{\prime \prime}+2 x y^{\prime}+4 y=0
  11. x2(1−x)y′′+(x−2)y′−3xy=0x^{2}(1-x) y^{\prime \prime}+(x-2) y^{\prime}-3 x y=0
  12. x2(1−x2)y′′+(2x)y′+4y=0x^{2}\left(1-x^{2}\right) y^{\prime \prime}+\left(\frac{2}{x}\right) y^{\prime}+4 y=0
  13. (1−x2)2y′′+x(1−x)y′+(1+x)y=0\left(1-x^{2}\right)^{2} y^{\prime \prime}+x(1-x) y^{\prime}+(1+x) y=0
  14. x2y′′+xy′+(x2−ν2)y=0x^{2} y^{\prime \prime}+x y^{\prime}+\left(x^{2}-\nu^{2}\right) y=0 \quad (贝塞尔方程)
  15. (x+2)2(x−1)y′′+3(x−1)y′−2(x+2)y=0(x+2)^{2}(x-1) y^{\prime \prime}+3(x-1) y^{\prime}-2(x+2) y=0
  16. x(3−x)y′′+(x+1)y′−2y=0x(3-x) y^{\prime \prime}+(x+1) y^{\prime}-2 y=0
  17. xy′′+exy′+(3cos⁡x)y=0x y^{\prime \prime}+e^{x} y^{\prime}+(3 \cos x) y=0
  18. y′′+(ln⁡∣x∣)y′+3xy=0y^{\prime \prime}+(\ln |x|) y^{\prime}+3 x y=0
  19. (sin⁡x)y′′+xy′+4y=0(\sin x) y^{\prime \prime}+x y^{\prime}+4 y=0
  20. (xsin⁡x)y′′+3y′+xy=0(x \sin x) y^{\prime \prime}+3 y^{\prime}+x y=0
  21. 找出 α\alpha 的所有值，使得 x→0x \rightarrow 0 时，x2y′′+αxy′+52y=0x^{2} y^{\prime \prime}+\alpha x y^{\prime}+\frac{5}{2} y=0 的所有解都趋于零。
  22. 找出 β\beta 的所有值，使得 x→0x \rightarrow 0 时，x2y′′+βy=0x^{2} y^{\prime \prime}+\beta y=0 的所有解都趋于零。
  23. 找出 γ\gamma，使得初值问题 x2y′′−2y=0,y(1)=1,y′(1)=γx^{2} y^{\prime \prime}-2 y=0, y(1)=1, y^{\prime}(1)=\gamma 的解在 x→0x \rightarrow 0 时是有界的。
  24. 考虑欧拉方程 x2y′′+αxy′+βy=0x^{2} y^{\prime \prime}+\alpha x y^{\prime}+\beta y=0。找出 α\alpha 和 β\beta 满足的条件，使得： a. 所有解在 x→0x \rightarrow 0 时趋于零。 b. 所有解在 x→0x \rightarrow 0 时是有界的。 c. 所有解在 x→∞x \rightarrow \infty 时趋于零。 d. 所有解在 x→∞x \rightarrow \infty 时是有界的。 e. 所有解在 x→0x \rightarrow 0 和 x→∞x \rightarrow \infty 时都是有界的。
  25. 使用降阶法，证明如果 r1r_{1} 是

r(r−1)+αr+β=0r(r-1)+\alpha r+\beta=0

的重根，则 xr1x^{r_{1}} 和 xr1ln⁡xx^{r_{1}} \ln x 是 x2y′′+αxy′+βy=0x^{2} y^{\prime \prime}+\alpha x y^{\prime}+\beta y=0 (当 x>0x>0 时) 的解。 29. 验证 W[xλcos⁡(μln⁡x),xλsin⁡(μln⁡x)]=μx2λ−1W\left[x^{\lambda} \cos (\mu \ln x), x^{\lambda} \sin (\mu \ln x)\right]=\mu x^{2 \lambda-1}。 ”

在问题 30 和 31 中，证明点 x=0x=0 是一个正则奇点。在每个问题中，尝试找出 ∑n=0∞anxn\sum_{n=0}^{\infty} a_{n} x^{n} 形式的解。证明（除了常数倍）在问题 30 中只有唯一一个这种形式的非零解，而在问题 31 中没有这种形式的非零解。因此，在这两种情况下，都不能用这种方式找到通解。这对于具有奇点的方程来说是典型的。

  1. 2xy′′+3y′+xy=02 x y^{\prime \prime}+3 y^{\prime}+x y=0

  2. 2x2y′′+3xy′−(1+x)y=02 x^{2} y^{\prime \prime}+3 x y^{\prime}-(1+x) y=0

  3. 无穷远处的奇点。前面章节中给出的常点和正则奇点的定义仅适用于点 x0x_{0} 是有限的情况。在微分方程的更高级的研究中，通常需要考虑无穷远处的点。这可以通过进行变量替换 ξ=1/x\xi=1/x 并研究在 ξ=0\xi=0 处得到的方程来实现。证明对于微分方程

P(x)y′′+Q(x)y′+R(x)y=0,P(x) y^{\prime \prime}+Q(x) y^{\prime}+R(x) y=0,

如果

1P(1/ξ)(2P(1/ξ)ξ−Q(1/ξ)ξ2) 和 R(1/ξ)ξ4P(1/ξ)\frac{1}{P(1 / \xi)}\left(\frac{2 P(1 / \xi)}{\xi}-\frac{Q(1 / \xi)}{\xi^{2}}\right) \text { 和 } \frac{R(1 / \xi)}{\xi^{4} P(1 / \xi)}

在 ξ=0\xi=0 附近具有泰勒级数展开，则无穷远处的点是常点。证明如果上述函数中至少有一个没有泰勒级数展开，但

ξP(1/ξ)(2P(1/ξ)ξ−Q(1/ξ)ξ2) 和 R(1/ξ)ξ2P(1/ξ)\frac{\xi}{P(1 / \xi)}\left(\frac{2 P(1 / \xi)}{\xi}-\frac{Q(1 / \xi)}{\xi^{2}}\right) \text { 和 } \frac{R(1 / \xi)}{\xi^{2} P(1 / \xi)}

都具有这样的展开，则无穷远处的点是一个正则奇点。

在问题 33 到 37 中，使用问题 32 的结果来确定无穷远处的点是给定的微分方程的常点、正则奇点还是非正则奇点。

  1. y′′+y=0y^{\prime \prime}+y=0

  2. x2y′′+xy′−4y=0x^{2} y^{\prime \prime}+x y^{\prime}-4 y=0

  3. (1−x2)y′′−2xy′+α(α+1)y=0\left(1-x^{2}\right) y^{\prime \prime}-2 x y^{\prime}+\alpha(\alpha+1) y=0 \quad (勒让德方程)

  4. y′′−2xy′+λy=0y^{\prime \prime}-2 x y^{\prime}+\lambda y=0 \quad (埃尔米特方程)

  5. y′′−xy=0y^{\prime \prime}-x y=0 (艾里方程)

请您提供需要处理的内容，我才能用 "" 为其中的名词加粗**，并保持原有格式，且不加粗符号公式。